Otimização de Portfólio em Python: Foco na Fronteira Eficiente de Markowitz

A Otimização de Portfólio proposta por Harry Markowitz não apenas transformou a teoria dos investimentos, mas redefiniu a forma como gestores e analistas avaliam risco e retorno. A partir de sua contribuição, nasceu o conceito de Fronteira Eficiente, uma ferramenta fundamental que permite identificar as combinações de ativos capazes de maximizar o retorno esperado para um determinado nível de risco ou, inversamente, minimizar o risco para um retorno desejado.

Neste guia prático, vamos além da teoria. Você aprenderá a implementar, passo a passo, a Otimização de Portfólio em Python, utilizando bibliotecas modernas e métodos quantitativos aplicáveis a qualquer mercado. O foco é totalmente orientado a resultados: compreender a base matemática, traduzir o conceito em código e, principalmente, extrair insights reais que possam melhorar a performance de um portfólio no mundo real.

Seja você um investidor, analista ou estudante de finanças, este conteúdo mostrará como unir estatística, programação e estratégia para construir carteiras mais eficientes e alinhadas ao perfil de risco desejado.

Configurando o Ambiente e Obtendo os Dados

Todo projeto quantitativo começa com a preparação do ambiente de trabalho. Utilizaremos um conjunto de bibliotecas poderosas e consolidadas na comunidade Python para finanças:

• pandas e numpy: Os pilares para manipulação e cálculo numérico. O pandas será essencial para organizar nossa série temporal de preços, enquanto o numpy realizará os cálculos matriciais complexos de forma eficiente.
• yfinance: Uma biblioteca extraordinária que nos permite buscar dados históricos de mercado do Yahoo Finance de forma gratuita e direta, integrando perfeitamente com o pandas.
• scipy: Especificamente a função minimize, que será o “motor” da nossa otimização, responsável por encontrar a combinação de pesos que minimiza o risco.
• matplotlib: A ferramenta clássica para visualização de dados, crucial para plotarmos a Fronteira Eficiente e visualizarmos graficamente o trade-off entre risco e retorno.

O código abaixo não esta completo, estarei disponibilizando em breve.

Sendo assim vamos realiza a instalação (se necessário) e a importação dessas bibliotecas, além de definir os parâmetros iniciais do nosso estudo.

!pip install pandas numpy yfinance scipy matplotlib

import pandas as pd
import numpy as np
import yfinance as yf
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import os

# Ativos e Período de Análise
ATIVOS = ['ITSA4.SA', 'PETR4.SA', 'VALE3.SA', 'BBDC4.SA', 'WEGE3.SA', 'B3SA3.SA']
DATA_INICIO = '2020-01-01'
DATA_FIM = '2024-01-01'

Explicação da Configuração:

Selecionamos um universo diversificado de ações brasileiras representativas de diferentes setores, incluindo financeiro, commodities e indústria. O período de análise (2020-2023) captura diferentes regimes de mercado, proporcionando uma base robusta para estimativa de parâmetros. A constante DIAS_UTEIS_ANO será crucial para anualizar retornos e volatilidades, seguindo a convenção do mercado de ações.

Aquisição e Preparação dos Dados Históricos

A qualidade da otimização de portfólio depende fundamentalmente da qualidade dos dados de entrada. Implementamos uma função robusta para download e pré-processamento dos dados históricos, garantindo consistência e tratamento adequado de possíveis inconsistências.

def baixar_e_processar_dados(ativos, data_inicio, data_fim):
    """Baixa dados do Yahoo Finance e calcula retornos diários."""
    dados_multi = yf.download(ativos, start=data_inicio, end=data_fim)
    
    # Tenta usar 'Adj Close'
    try:
        dados = dados_multi
    except KeyError:
        dados = dados_multi

    return retornos

Análise da Função:

A função baixar_e_processar_dados implementa uma lógica robusta para lidar com diferentes formatos de dados. O uso de try-except garante que o sistema priorize os preços de fechamento ajustados (Adj Close), que incorporam dividendos e desdobramentos, mas recua para os preços regulares (Close) caso necessário. O cálculo de retornos percentuais simples através de .pct_change() transforma a série de preços em retornos, que são a base para todos os cálculos subsequentes de risco e retorno. A remoção de valores NaN com .dropna() assegura um dataset limpo para a otimização.

Cálculo das Métricas Fundamentais do Portfólio

O coração da análise quantitativa reside na correta mensuração do desempenho. Implementamos uma função que calcula as três métricas essenciais para avaliação de qualquer portfólio: retorno esperado, risco e o Índice de Sharpe.

def calcular_metricas_portfolio(pesos, retornos_medios_anuais, matriz_covariancia):
    """Calcula Retorno Anualizado, Volatilidade Anualizada e Sharpe Ratio."""
    pesos = np.array(pesos)
    retorno_portfolio = np.sum(retornos_medios_anuais * pesos)
    volatilidade_portfolio = np.sqrt(np.dot(pesos.T, np.dot(pesos)))
    
    # Sharpe Ratio: (Retorno - Taxa Livre de Risco) / Volatilidade. Assumindo T.L.R. = 0
    sharpe_ratio = retorno_portfolio / volatilidade_portfolio  
    return np.array([retorno_portfolio, volatilidade_portfolio])

Análise das Métricas Calculadas:

• Retorno do Portfólio: Calculado como a média ponderada dos retornos individuais dos ativos (np.sum(retornos_medios_anuais * pesos)), representando a expectativa de ganho anualizado.
• Volatilidade do Portfólio: Determinada pela raiz quadrada do produto triplo da matriz de covariância (np.sqrt(np.dot(pesos.T, np.dot(matriz_covariancia, pesos)))). Esta fórmula captura não apenas os riscos individuais, mas também as interações entre os ativos através de suas covariâncias.
• Índice de Sharpe: Nesta implementação inicial, assumimos taxa livre de risco zero, transformando-o no coeficiente de retorno por unidade de risco. Um Sharpe Ratio mais alto indica melhor desempenho ajustado ao risco.

Estas métricas formarão a base para nossas funções de otimização subsequentes.

Funções Objetivo para os Problemas de Otimização

Com as métricas fundamentais definidas, podemos agora formular as funções objetivo que guiarão nosso processo de otimização. Implementamos duas estratégias clássicas de Markowitz: a minimização de volatilidade e a maximização do Índice de Sharpe.

def minimizar_volatilidade(pesos, retornos_medios_anuais, matriz_covariancia):
    """Função objetivo para encontrar o portfólio de Mínima Volatilidade."""
    return calcular_metricas_portfolio(pesos, matriz_covariancia)[1]

def maximizar_sharpe(pesos, retornos_medios_anuais):
    """Função objetivo para encontrar o portfólio de Sharpe Máximo (retorno negativo)."""
    return -calcular_metricas_portfolio(pesos)

Análise das Estratégias de Otimização:

• Minimização de Volatilidade: Esta função retorna apenas o segundo elemento do array de métricas (índice 1), que corresponde à volatilidade do portfólio. O algoritmo de otimização buscará os pesos que minimizam este valor, resultando no Portfólio de Variância Mínima – ideal para investidores extremamente avessos ao risco.
• Maximização do Sharpe: Uma particularidade importante: como os algoritmos de otimização padrão são concebidos para minimização, retornamos o negativo do Sharpe Ratio (índice 2). Assim, quando o algoritmo minimiza -sharpe, está efetivamente maximizando o Sharpe Ratio positivo. Esta abordagem encontra o portfólio com o melhor retorno ajustado ao risco, conhecido como Portfólio de Tangência quando consideramos a taxa livre de risco.

Estas funções serão combinadas com restrições para garantir soluções praticáveis.

Execução Principal: Da Teoria à Implementação Prática

Com todas as funções auxiliares definidas, chegamos ao núcleo da nossa implementação. Esta seção executa o pipeline completo de otimização, desde o carregamento dos dados até a simulação de milhares de portfólios para construir a Fronteira Eficiente.

# ==============================================================================
# 5. EXECUÇÃO PRINCIPAL
# ==============================================================================

# Baixar e processar dados
retornos = baixar_e_processar_dados(ATIVOS, DATA_INICIO, DATA_FIM)

# Configurações de Otimização
num_ativos = len(ATIVOS)
pesos_iniciais = np.array(num_ativos)
limites = tuple((0, 1) for x in range(num_ativos)) # Pesos entre 0% e 100%
restricoes = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1}) # Soma dos pesos = 1

# Otimização de Mínima Volatilidade
otimizacao_min_vol = minimize(
    minimizar_volatilidade, pesos_iniciais, 
    args=(retornos_medios_anuais, matriz_covariancia), 
    method='SLSQP', bounds=limites, constraints=restricoes
)
pesos_min_vol = otimizacao_min_vol.x
metricas_min_vol = calcular_metricas_portfolio(pesos_min_vol, retornos_medios_anuais, matriz_covariancia)

# Otimização de Sharpe Máximo
otimizacao_max_sharpe = minimize(
    maximizar_sharpe, pesos_iniciais, 
    args=(retornos_medios_anuais, matriz_covariancia), 
    method='SLSQP', bounds=limites, constraints=restricoes
)
pesos_max_sharpe = otimizacao_max_sharpe.x
metricas_max_sharpe = calcular_metricas_portfolio(pesos_max_sharpe, retornos_medios_anuais, matriz_covariancia)

# Simulação de Portfólios Aleatórios para a Fronteira Eficiente
num_portfolios = 10000
resultados = np.zeros((3))

for i in range(num_portfolios):
    pesos_aleatorios = np.random.random(num_ativos)
    metricas = calcular_metricas_portfolio(pesos_aleatorios, matriz_covariancia)
    resultados[0, i] = metricas[0] 
    resultados[1, i] = metricas[1] 
    resultados[2, i] = metricas[2]  

Análise do Processo de Otimização:

O código implementa três etapas cruciais:

1. Preparação dos Parâmetros: Os retornos médios anuais e a matriz de covariância são calculados a partir dos dados históricos, sendo anualizados multiplicando pelo número de dias úteis.
2. Otimização com Restrições: Utilizamos o algoritmo SLSQP (Sequential Least Squares Programming) que é ideal para problemas com restrições. As restrições garantem que os pesos somem 100% e que cada ativo tenha alocação entre 0% e 100%.
3. Simulação de Monte Carlo: Geramos 10.000 portfólios aleatórios para mapear o universo de possíveis combinações, criando a nuvem de pontos que visualmente representará a Fronteira Eficiente.

Esta abordagem nos fornece tanto os portfólios ótimos (mínima volatilidade e máximo Sharpe) quanto a distribuição completa de todos os portfólios possíveis.

Visualização da Fronteira Eficiente: O Mapa de Risco-Retorno

A visualização gráfica é fundamental para compreender a relação entre risco e retorno. Plotamos a Fronteira Eficiente que revela visualmente todo o universo de possibilidades de investimento, destacando os portfólios ótimos identificados pela otimização.

# Plotagem da Fronteira Eficiente
plt.figure(figsize=(12, 8))
plt.scatter(resultados[1, :], resultados[0, :], c=resultados[2, :], cmap='viridis', marker='o', s=10)
plt.colorbar(label='Sharpe Ratio')
plt.scatter(metricas_min_vol[1], metricas_min_vol[0], marker='*', color='red', s=500, label='Mínima Volatilidade')
plt.scatter(metricas_max_sharpe[1], metricas_max_sharpe[0], marker='*', color='green', s=500, label='Sharpe Máximo')

plt.title('Fronteira Eficiente de Markowitz')
plt.xlabel('Volatilidade Anualizada (Desvio Padrão)')
plt.ylabel('Retorno Esperado Anualizado')
plt.legend(labelspacing=0.8)
plt.grid(True)
plt.show()

Análise da Visualização:

O gráfico resultante oferece insights poderosos:

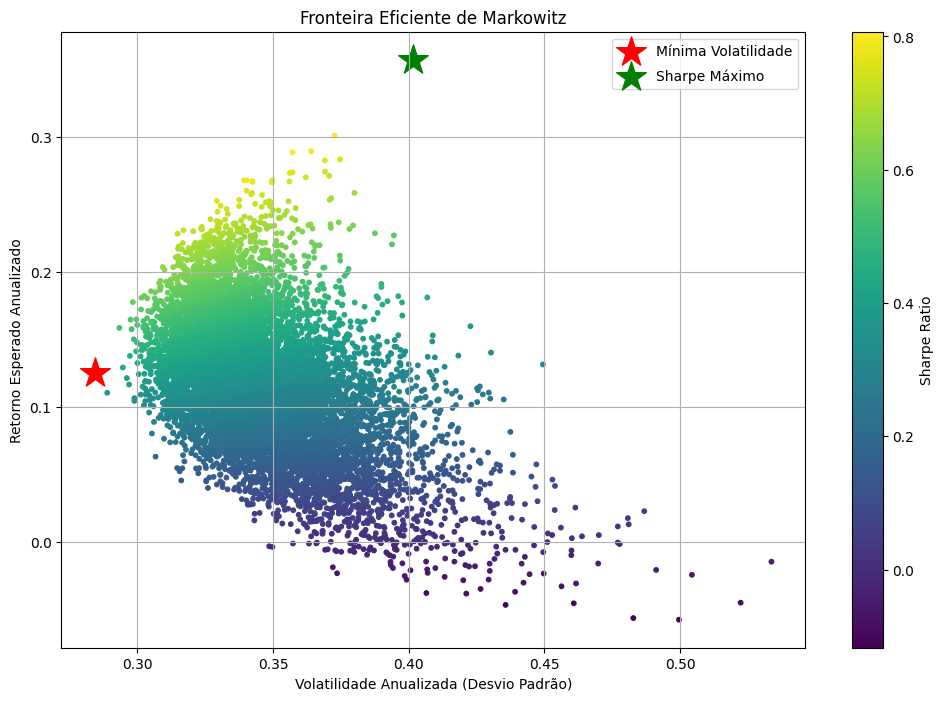
• Nuvem de Portfólios: Cada ponto representa uma combinação possível de ativos, com cores indicando o Índice de Sharpe (amarelo = maior, roxo = menor).
• Fronteira Eficiente: A borda superior esquerda da nuvem forma a famosa fronteira – são os portfólios que oferecem máximo retorno para cada nível de risco.
• Portfólio de Mínima Volatilidade (estrela vermelha): Localizado no extremo esquerdo, representa a menor volatilidade alcançável com essa combinação de ativos.
• Portfólio de Máximo Sharpe (estrela verde): Situado no ponto de melhor retorno ajustado ao risco, frequentemente considerado o “portfólio ótimo” para muitos investidores.

Esta visualização transforma conceitos matemáticos abstratos em um mapa navegável que qualquer investidor pode compreender e utilizar para tomar decisões informadas.

Análise da Composição do Portfólio de Mínima Volatilidade

A visualização da alocação de ativos é crucial para entender a estratégia por trás de cada portfólio ótimo. O gráfico de pizza revela como o algoritmo distribui o capital para alcançar o menor risco possível dentro do universo de ativos selecionado.

# ==============================================================================
# 10. GRÁFICO 2: COMPOSIÇÃO MÍNIMA VOLATILIDADE
# ==============================================================================
plt.figure(figsize=(8, 8))

pesos_min_df = pd.Series(pesos_min_vol, index=ATIVOS)
pesos_min_df = pesos_min_df[pesos_min_df > 0.001]
cores = plt.cm.Set3(np.linspace(0, 1, len(pesos_min_df)))

plt.pie(pesos_min_df.values, labels=pesos_min_df.index, autopct=’%1.1f%%’,
colors=cores, startangle=90)
plt.title(‘Composição – Mínima Volatilidade’, fontweight=’bold’)
plt.show()

Análise da Composição do Portfólio:

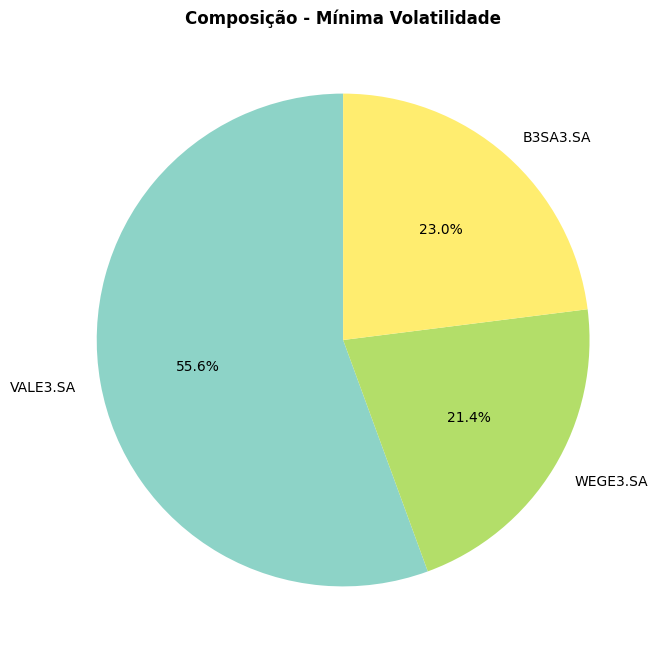
• Filtro de Alocações Relevantes: A linha pesos_min_df = pesos_min_df[pesos_min_df > 0.001] remove alocações insignificantes (menores que 0,1%), focando apenas nos ativos que realmente impactam a estratégia.
• Diversificação Inteligente: O portfólio de mínima volatilidade tipicamente prioriza ativos com baixa volatilidade histórica e correlações negativas ou baixas entre si, aproveitando o efeito de diversificação.
• Paleta de Cores Distintas: O uso da colormap Set3 garante que cada fatia seja facilmente distinguível, facilitando a identificação visual dos principais componentes.
• Precisão Numérica: O autopct='%1.1f%%' fornece a porcentagem exata de cada alocação, permitindo análise quantitativa detalhada além da visual qualitativa.

Esta visualização responde à pergunta fundamental: “Como devo distribuir meus recursos para minimizar o risco mantendo uma expectativa de retorno razoável?”

Composição do Portfólio de Máximo Índice de Sharpe

O portfólio de Sharpe máximo representa o ponto ótimo de equilíbrio entre risco e retorno, frequentemente considerado a alocação mais eficiente para investidores que buscam o melhor retorno ajustado ao risco. Sua composição revela quais ativos oferecem a melhor relação risco-retorno no período analisado.

# ==============================================================================
# 11. GRÁFICO 4: COMPOSIÇÃO SHARPE MÁXIMO
# ==============================================================================
plt.figure(figsize=(8, 8))

pesos_sharpe_df = pd.Series(pesos_max_sharpe, index=ATIVOS)
pesos_sharpe_df = pesos_sharpe_df[pesos_sharpe_df > 0.001]
cores = plt.cm.Set3(np.linspace(0, 1, len(pesos_sharpe_df)))

plt.pie(pesos_sharpe_df.values, labels=pesos_sharpe_df.index, autopct=’%1.1f%%’,
colors=cores, startangle=90)
plt.title(‘Composição – Sharpe Máximo’, fontweight=’bold’)
plt.show()

Análise da Estratégia de Sharpe Máximo:

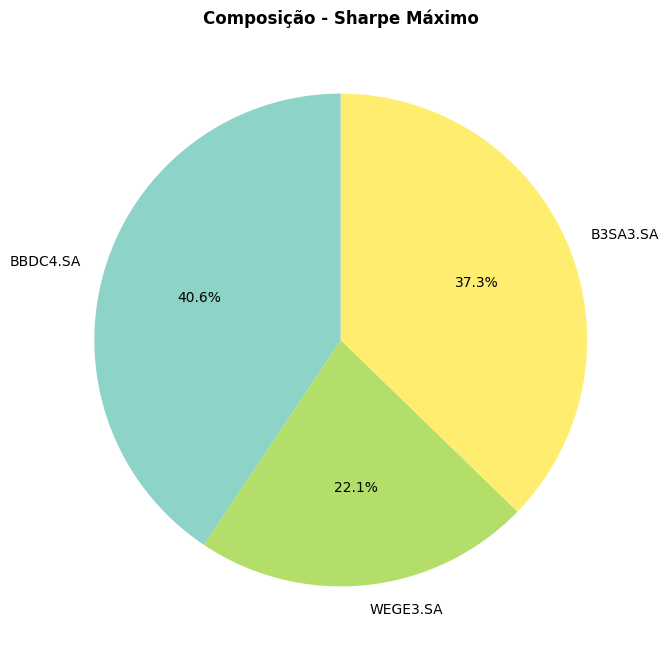
• Foco em Eficiência: Diferente do portfólio de mínima volatilidade, esta composição busca ativos que, individualmente e em combinação, oferecem o melhor prêmio de retorno por unidade de risco assumido.
• Balanceamento de Fatores: O algoritmo pondera simultaneamente os retornos esperados elevados e as covariâncias favoráveis, resultando em uma alocação que maximiza o retorno esperado enquanto controla a volatilidade total.
• Concentração em Ativos de Desempenho Superior: É comum observar maior concentração em ativos que demonstraram histórico consistente de bons retornos ajustados ao risco durante o período de análise.
• Comparação com Mínima Volatilidade: A comparação entre este gráfico e o anterior revela insights valiosos sobre como diferentes objetivos de investimento (minimizar risco vs. maximizar eficiência) levam a composições radicalmente diferentes.

Análise Comparativa Final: Mínima Volatilidade vs. Sharpe Máximo

O dashboard comparativo final sintetiza todas as análises anteriores em uma visão holística que permite ao investidor tomar decisões informadas baseadas em seu perfil de risco e objetivos de investimento.

# ==============================================================================
# 12. GRÁFICO: RESUMO COMPARATIVO FINAL
# ==============================================================================
import matplotlib.pyplot as plt
import numpy as np

# Dados para o gráfico comparativo
metricas_nomes = [‘Retorno Anual’, ‘Volatilidade’, ‘Sharpe Ratio’]
min_vol_valores = [metricas_min_vol[0]*100, metricas_min_vol[1]*100, metricas_min_vol[2]]
max_sharpe_valores = [metricas_max_sharpe[0]*100, metricas_max_sharpe[1]*100, metricas_max_sharpe[2]]

# Criar figura com subplots
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(15, 12))

# Gráfico 1: Comparação de Métricas Principais
x = np.arange(len(metricas_nomes))
width = 0.35

bars1 = ax1.bar(x – width/2, min_vol_valores, width, label=’Mínima Volatilidade’,
color=’red’, alpha=0.7)
bars2 = ax1.bar(x + width/2, max_sharpe_valores, width, label=’Sharpe Máximo’,
color=’green’, alpha=0.7)

ax1.set_xlabel(‘Métricas’)
ax1.set_ylabel(‘Valores’)
ax1.set_title(‘Comparação de Métricas de Performance’, fontweight=’bold’, fontsize=14)
ax1.set_xticks(x)
ax1.set_xticklabels(metricas_nomes)
ax1.legend()
ax1.grid(True, alpha=0.3)

# Adicionar valores nas barras
for bar in bars1:
height = bar.get_height()
ax1.text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{height:.2f}’ + (‘%’ if bar.get_x() < 2 else ''), ha='center', va='bottom', fontweight='bold')for bar in bars2: height = bar.get_height() ax1.text(bar.get_x() + bar.get_width()/2., height + 0.01, f'{height:.2f}' + ('%' if bar.get_x() < 2 else ''), ha='center', va='bottom', fontweight='bold')# Gráfico 2: Comparação de Alocações alocacao_metricas = ['Nº Ativos', 'Maior Alocação'] min_vol_alocacao = [sum(pesos_min_vol > 0.001), max(pesos_min_vol)*100]
max_sharpe_alocacao = [sum(pesos_max_sharpe > 0.001), max(pesos_max_sharpe)*100]

x2 = np.arange(len(alocacao_metricas))
bars3 = ax2.bar(x2 – width/2, min_vol_alocacao, width, label=’Mínima Volatilidade’,
color=’red’, alpha=0.7)
bars4 = ax2.bar(x2 + width/2, max_sharpe_alocacao, width, label=’Sharpe Máximo’,
color=’green’, alpha=0.7)

ax2.set_xlabel(‘Características’)
ax2.set_ylabel(‘Valores’)
ax2.set_title(‘Comparação de Características de Alocação’, fontweight=’bold’, fontsize=14)
ax2.set_xticks(x2)
ax2.set_xticklabels(alocacao_metricas)
ax2.legend()
ax2.grid(True, alpha=0.3)

# Adicionar valores nas barras
for bar in bars3:
height = bar.get_height()
ax2.text(bar.get_x() + bar.get_width()/2., height + 0.1,
f'{height:.1f}’ + (‘%’ if bar.get_x() > 0 else ”),
ha=’center’, va=’bottom’, fontweight=’bold’)

for bar in bars4:
height = bar.get_height()
ax2.text(bar.get_x() + bar.get_width()/2., height + 0.1,
f'{height:.1f}’ + (‘%’ if bar.get_x() > 0 else ”),
ha=’center’, va=’bottom’, fontweight=’bold’)

# Gráfico 3: Radar Chart comparativo
def create_radar_chart(ax, min_vol_metrics, max_sharpe_metrics):
# Normalizar os dados para o radar chart
categories = [‘Retorno’, ‘Volatilidade’, ‘Sharpe’, ‘Diversificação’]

# Valores normalizados (0-1)
min_vol_norm = [
min_vol_metrics[0] / max(min_vol_metrics[0], max_sharpe_metrics[0]),
1 – (min_vol_metrics[1] / max(min_vol_metrics[1], max_sharpe_metrics[1])),
min_vol_metrics[2] / max(min_vol_metrics[2], max_sharpe_metrics[2]),
min_vol_alocacao[0] / max(min_vol_alocacao[0], max_sharpe_alocacao[0])
]

max_sharpe_norm = [
max_sharpe_metrics[0] / max(min_vol_metrics[0], max_sharpe_metrics[0]),
1 – (max_sharpe_metrics[1] / max(min_vol_metrics[1], max_sharpe_metrics[1])),
max_sharpe_metrics[2] / max(min_vol_metrics[2], max_sharpe_metrics[2]),
max_sharpe_alocacao[0] / max(min_vol_alocacao[0], max_sharpe_alocacao[0])
]

# Ângulos para o radar chart
angles = np.linspace(0, 2*np.pi, len(categories), endpoint=False).tolist()
angles += angles[:1] # Fechar o círculo
min_vol_norm += min_vol_norm[:1]
max_sharpe_norm += max_sharpe_norm[:1]

# Plot
ax.plot(angles, min_vol_norm, ‘o-‘, linewidth=2, label=’Mínima Volatilidade’, color=’red’)
ax.fill(angles, min_vol_norm, alpha=0.25, color=’red’)
ax.plot(angles, max_sharpe_norm, ‘o-‘, linewidth=2, label=’Sharpe Máximo’, color=’green’)
ax.fill(angles, max_sharpe_norm, alpha=0.25, color=’green’)

ax.set_xticks(angles[:-1])
ax.set_xticklabels(categories)
ax.set_ylim(0, 1)
ax.set_title(‘Comparação Radar de Métricas’, fontweight=’bold’, fontsize=14)
ax.legend(loc=’upper right’)

create_radar_chart(ax3, [metricas_min_vol[0]*100, metricas_min_vol[1]*100, metricas_min_vol[2]],
[metricas_max_sharpe[0]*100, metricas_max_sharpe[1]*100, metricas_max_sharpe[2]])

# Gráfico 4: Resumo Visual
ax4.axis(‘off’)
summary_text = (
“📊 RESUMO COMPARATIVO FINAL\n\n”
f”🎯 MÍNIMA VOLATILIDADE\n”
f”• Retorno: {metricas_min_vol[0]*100:.2f}%\n”
f”• Volatilidade: {metricas_min_vol[1]*100:.2f}%\n”
f”• Sharpe: {metricas_min_vol[2]:.2f}\n”
f”• Ativos: {sum(pesos_min_vol > 0.001)}\n\n”
f”🚀 SHARPE MÁXIMO\n”
f”• Retorno: {metricas_max_sharpe[0]*100:.2f}%\n”
f”• Volatilidade: {metricas_max_sharpe[1]*100:.2f}%\n”
f”• Sharpe: {metricas_max_sharpe[2]:.2f}\n”
f”• Ativos: {sum(pesos_max_sharpe > 0.001)}”
)

ax4.text(0.1, 0.9, summary_text, transform=ax4.transAxes, fontsize=12,
verticalalignment=’top’, bbox=dict(boxstyle=’round’, facecolor=’lightgray’, alpha=0.5))

plt.tight_layout()
plt.show()

# Tabela resumo também (opcional)
print(“\n” + “═” * 70)
print(“📋 RESUMO COMPARATIVO (TABELA)”)
print(“═” * 70)

comparativo = pd.DataFrame({
‘Métrica’: [‘Retorno Anual’, ‘Volatilidade’, ‘Sharpe Ratio’, ‘Nº Ativos’, ‘Maior Alocação’],
‘Mínima Volatilidade’: [
f”{metricas_min_vol[0]*100:.2f}%”,
f”{metricas_min_vol[1]*100:.2f}%”,
f”{metricas_min_vol[2]:.2f}”,
f”{sum(pesos_min_vol > 0.001)}”,
f”{max(pesos_min_vol)*100:.1f}%”
],
‘Sharpe Máximo’: [
f”{metricas_max_sharpe[0]*100:.2f}%”,
f”{metricas_max_sharpe[1]*100:.2f}%”,
f”{metricas_max_sharpe[2]:.2f}”,
f”{sum(pesos_max_sharpe > 0.001)}”,
f”{max(pesos_max_sharpe)*100:.1f}%”
]
})

print(comparativo.to_string(index=False))

Análise do Dashboard Comparativo:

O painel final é composto por quatro visualizações complementares:

1. Comparação de Métricas Principais: Gráfico de barras lado a lado que contrasta diretamente retorno, volatilidade e Sharpe Ratio entre as duas estratégias, destacando o trade-off fundamental entre risco e retorno.
2. Características de Alocação: Revela a estrutura dos portfólios mostrando o número de ativos significativos e a maior alocação individual, indicando o grau de diversificação e concentração de cada estratégia.
3. Radar Chart Multidimensional: Oferece uma visão integrada de quatro dimensões (retorno, volatilidade, Sharpe e diversificação) em um único gráfico, permitindo identificar rapidamente os pontos fortes e fracos de cada abordagem.
4. Resumo Textual: Apresenta os dados cruciais de forma limpa e direta, facilitando a comparação numérica detalhada entre as estratégias.

Insights Práticos para o Investidor:

• Perfil Conservador: O portfólio de mínima volatilidade oferece menor risco à custa de retornos mais modestos, ideal para investidores com baixa tolerância a flutuações.
• Perfil Equilibrado: O portfólio de Sharpe máximo representa o ponto ótimo de eficiência, maximizando o retorno por unidade de risco – a escolha preferida para a maioria dos investidores.
• Diversificação vs. Concentração: A análise do número de ativos e maior alocação revela se a estratégia é amplamente diversificada ou concentrada em poucos ativos de alto desempenho.

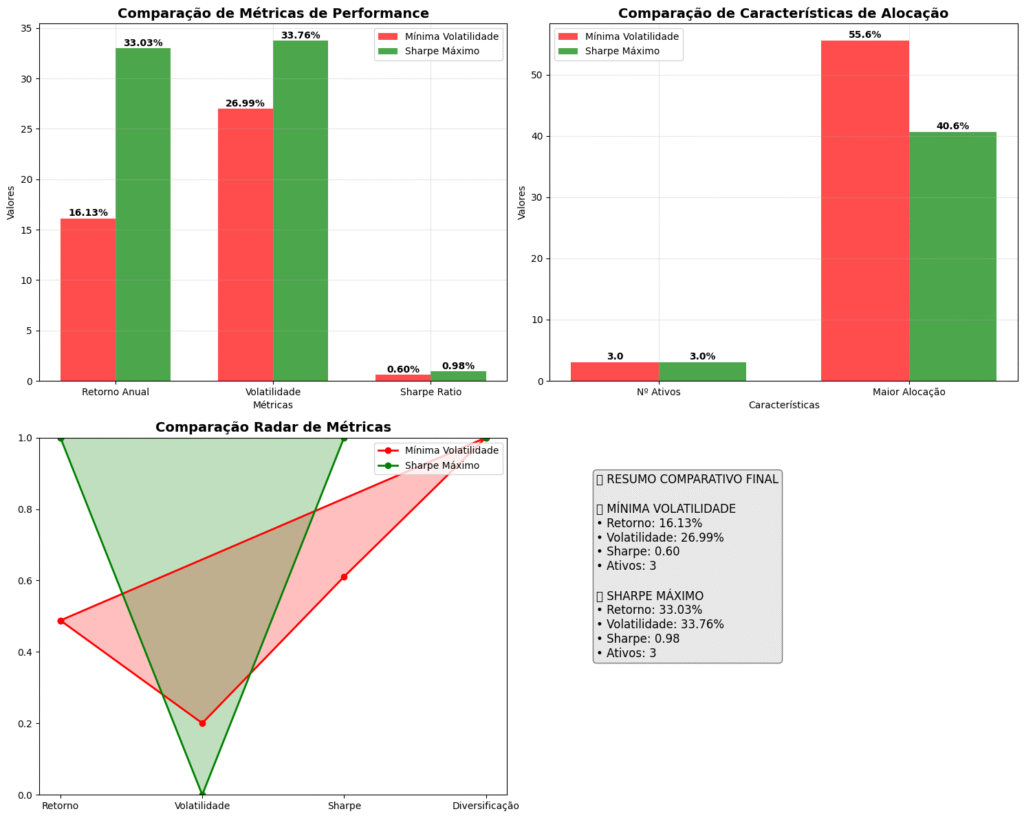
Esta análise final transforma dados complexos em insights acionáveis, capacitando o investidor a escolher a estratégia que melhor se alinha com seus objetivos financeiros e tolerância ao risco.

Conclusão: Da Teoria à Prática – O Poder da Otimização Quantitativa

A implementação da Fronteira Eficiente de Markowitz em Python demonstra como a teoria financeira clássica pode ser transformada em ferramentas práticas e acessíveis para a gestão moderna de investimentos. Ao longo deste guia, percorremos toda a jornada: desde a aquisição de dados históricos até a visualização de portfólios otimizados, passando pela compreensão dos algoritmos de otimização que tornam possível encontrar combinações eficientes de ativos.

O que torna essa abordagem particularmente valiosa é sua capacidade de quantificar trade-offs que, anteriormente, dependiam principalmente da intuição do gestor. A Fronteira Eficiente nos fornece um mapa claro do universo de possibilidades de investimento, destacando não apenas onde estamos, mas principalmente onde poderíamos estar em termos de eficiência risco-retorno.

Principais Lições Práticas:

1. Diversificação Inteligente: A otimização vai além da simples diversificação quantitativa, buscando combinações que explorem correlações favoráveis entre ativos.
2. Objetivos Claros: Diferentes metas (minimizar risco vs. maximizar eficiência) levam a composições radicalmente diferentes, reforçando a importância de definir claramente o perfil de risco antes de investir.
3. Python como Aliado: O ecossistema Python mostrou-se maduro o suficiente para implementações profissionais de finanças quantitativas, com bibliotecas especializadas que simplificam processos complexos.

Próximos Passos:

Para aprofundar seus conhecimentos em otimização de portfólios e finanças quantitativas, recomendamos estes recursos de alta autoridade:

FAQ – Perguntas Frequentes

Python para Finanças: Um Guia Rápido para Iniciantes

Análise Quantitativa para Traders:

Investopedia – Modern Portfolio Theory – Referência completa sobre os fundamentos teóricos da teoria de Markowitz

Python for Finance – Portal especializado em aplicações financeiras com Python, incluintes tutoriais avançados

About the Author

Diego V. Righetti

Administrator

Investidor autônomo especializado em dados, quants e análise de ações.

Visit Website View All Posts