Nota do autor: Este artigo é a continuação da nossa série sobre otimização de portfólios. Se você ainda não leu, recomendamos começar pelo nosso artigo anterior sobre a Otimização de Portfólio: Fronteira Eficiente (Markowitz) para uma base completa.
No mundo dos investimentos, a busca por retornos é uma jornada constante, mas o verdadeiro domínio do mercado financeiro não reside apenas em maximizar ganhos, e sim em gerenciar os riscos de forma inteligente. Após explorarmos como construir uma carteira otimizada através da fronteira eficiente de Markowitz, é hora de darmos um passo adiante e mergulharmos nas ferramentas que nos permitem quantificar e controlar as possíveis perdas: o Value at Risk (VaR) e o Conditional Value at Risk (CVaR).
Enquanto a otimização de Markowitz nos ajuda a montar um portfólio com a melhor relação risco-retorno esperada, o VaR e CVaR nos oferecem uma perspectiva crucial sobre o que pode acontecer nos cenários adversos. Eles respondem a uma pergunta fundamental para qualquer investidor: “Qual é a perda máxima que eu posso esperar em minha carteira, com um determinado nível de confiança?”
Neste artigo, vamos desmistificar o VaR e o CVaR, saindo da teoria para a prática. Utilizando Python, vamos construir um sistema de análise de risco do zero, capaz de calcular essas métricas essenciais e apresentar os resultados em um dashboard completo e intuitivo. Você aprenderá não apenas o que são o VaR e o CVaR, mas também como implementá-los e interpretá-los para tomar decisões de investimento mais seguras e bem-informadas.
Se você é um investidor que busca aprimorar sua gestão de risco, um estudante de finanças ou um entusiasta de Python querendo aplicar suas habilidades no mercado financeiro, este artigo é para você. Vamos juntos transformar dados em decisões e incerteza em estratégia.
O Que São VaR e CVaR? Desvendando as Métricas de Risco
Antes de mergulharmos no código, é crucial entender o que o VaR e o CVaR representam. Imagine que você está planejando uma viagem e o meteorologista informa que há 95% de chance de a temperatura não cair abaixo de 10°C. Essa é a ideia central do Value at Risk (VaR).
O Value at Risk (VaR) é uma medida estatística que estima a perda máxima potencial de um investimento ou portfólio ao longo de um determinado período de tempo, para um dado nível de confiança.
Por exemplo, se um portfólio tem um VaR de 1 dia de R$ 1 milhão com 95% de confiança, isso significa que há uma probabilidade de 5% de que as perdas do portfólio excedam R$ 1 milhão em um único dia. É uma única métrica que resume o risco de cauda de uma carteira. O CFA Institute sobre gestão de risco de mercado define o VaR como “a perda mínima… que seria esperada ser incorrida em uma certa porcentagem do tempo, durante um certo período de tempo, dadas as condições de mercado assumidas”.
No entanto, o VaR tem uma limitação importante: ele não nos diz nada sobre o quão grandes as perdas podem ser quando esse limite de 5% é ultrapassado. É aqui que entra o Conditional Value at Risk (CVaR).
O Conditional Value at Risk (CVaR), também conhecido como Expected Shortfall (Perda Esperada), vai um passo além. Ele calcula a perda média esperada, dado que a perda já excedeu o valor do VaR.
Em outras palavras, o CVaR responde à pergunta: “Se eu tiver um dia ruim (além do meu VaR), qual será a minha perda média nesse cenário?”. Como destaca a Investopedia sobre Conditional Value at Risk, o CVaR quantifica as perdas esperadas que ocorrem além do ponto de ruptura do VaR, oferecendo uma visão mais completa do risco de cauda.
| Métrica | Pergunta que Responde | Foco | Limitação |
| VaR | Qual a minha perda máxima esperada em X% dos cenários? | Ponto de corte da perda | Não informa sobre a magnitude das perdas além do seu limite. |
| CVaR | Se eu ultrapassar minha perda máxima esperada, qual será a perda média? | Média das perdas extremas | É uma média, e perdas individuais podem ser ainda maiores. |
Compreender tanto o VaR quanto o CVaR é fundamental para uma gestão de risco robusta, pois juntos eles fornecem um panorama mais claro dos riscos que uma carteira enfrenta, especialmente em condições de mercado voláteis.
Vamos colocar as Mãos na Obra!
Construindo a Análise de Risco com Python
Agora que os conceitos de VaR e CVaR estão claros, vamos ao que interessa: traduzir essa teoria em um código funcional. Nosso objetivo é criar um sistema que, a partir de uma lista de ativos, baixe os dados do mercado, calcule os retornos e, em seguida, aplique os métodos de VaR e CVaR para quantificar o risco.
Vamos dividir o código em partes para facilitar o entendimento.
Vamos a partes do Codigo vou liberar ele completo em breve
Parte 1: Configuração Inicial e Coleta de Dados
Todo projeto de análise de dados começa com a preparação do ambiente e a coleta das informações. Aqui, definimos as bibliotecas que usaremos, os ativos da nossa carteira, o período de análise e os parâmetros de risco.
# ==============================================================================
# 1. IMPORTAÇÃO DE BIBLIOTECAS E CONFIGURAÇÕES INICIAIS
# ==============================================================================
import pandas as pd
import numpy as np
import yfinance as yf
from scipy.stats import norm
# Ativos, Período e Parâmetros de Risco
ATIVOS = ['WEGE3.SA', 'PETR4.SA', 'VALE3.SA', 'BBDC4.SA']
DATA_INICIO = '2023-01-01'
DATA_FIM = '2025-01-01'
Neste trecho, estamos importando bibliotecas essenciais:
• Pandas e NumPy: Para manipulação e operações com dados.
• yfinance: Uma biblioteca fantástica que nos permite baixar dados históricos de mercado
• scipy.stats.norm: Usaremos para acessar a função de distribuição normal, crucial para o cálculo do VaR Paramétrico.
Em seguida, definimos um portfólio hipotético com quatro grandes empresas da bolsa brasileira (WEGE, Petrobras, Vale e Bradesco), um período de análise de dois anos e um nível de confiança de 95%, que é um padrão comum no mercado.
Parte 2: Calculando os Retornos do Portfólio
Com os ativos definidos, o próximo passo é obter seus preços de fechamento e calcular os retornos diários da nossa carteira. Para simplificar, vamos assumir uma carteira com pesos iguais para cada ativo.
# ==============================================================================
# 2. FUNÇÃO: DOWNLOAD E CÁLCULO DE RETORNOS DO PORTFÓLIO
# ==============================================================================
def calcular_retornos_portfolio(ativos, data_inicio, data_fim):
"""Baixa dados, calcula retornos e retorna os retornos do portfólio (pesos iguais)."""
dados_multi = yf.download(ativos, start=data_inicio, end=data_fim)
try:
dados = dados_multi['Adj Close']
except KeyError:
retornos = dados.pct_change()
# Pesos iguais para simplificação
num_ativos = len(ativos)
retornos_portfolio = retornos.dot(pesos)
return retornos_portfolio, pesos
A função calcular_retornos_portfolio é o coração da nossa coleta de dados. Ela:
1.Usa yf.download() para baixar os preços de fechamento ajustados (Adj Close) dos ativos.
2.Calcula os retornos diários com pct_change().
3.Define um vetor de pesos iguais (neste caso, 25% para cada um dos quatro ativos).
4.Calcula os retornos diários do portfólio através de um produto escalar (dot) entre os retornos dos ativos e seus respectivos pesos. O resultado é uma série temporal que representa o desempenho diário da nossa carteira consolidada.
Com os retornos do portfólio em mãos, temos a matéria-prima para começar a calcular nossas métricas de risco: VaR e CVaR.
Parte 3: Calculando o VaR Paramétrico e o VaR/CVaR Histórico
Com a série de retornos da nossa carteira, podemos finalmente calcular o VaR e o CVaR. Vamos explorar duas abordagens populares: a paramétrica (ou Gaussiana) e a histórica.
O Método Paramétrico: A Curva Normal em Ação
Este método assume que os retornos do portfólio seguem uma distribuição normal (a famosa curva de sino). Embora seja uma simplificação, é um método rápido e amplamente utilizado para uma primeira avaliação do risco.
# ==============================================================================
# 3. FUNÇÃO: CÁLCULO DO VaR PARAMÉTRICO (GAUSSIANO)
# ==============================================================================
def calcular_var_parametrico(retornos_portfolio, confianca, horizonte_dias):
"""Calcula o VaR Paramétrico (Gaussiano) para o horizonte de dias."""
media_retorno = retornos_portfolio.mean()
# VaR Diário (em termos de retorno)
var_retorno_param = media_retorno - z_score * desvio_padrao
# VaR em termos de perda, ajustado para o horizonte (regra do sqrt(t))
var_param_perda = -var_retorno_param * np.sqrt(horizonte_dias)
return var_param_perda
A lógica aqui é puramente estatística:
1.Calculamos a média (mean) e o desvio padrão (std) dos retornos diários do nosso portfólio.
2.Usamos norm.ppf(confianca) para encontrar o Z-score correspondente ao nosso nível de confiança. O Z-score nos diz quantos desvios padrão da média precisamos nos afastar para capturar a área desejada sob a curva normal.
3.A fórmula media_retorno – z_score * desvio_padrao nos dá o ponto de corte do VaR na distribuição de retornos.
4.Finalmente, multiplicamos pelo sinal negativo para representar o valor como uma perda e ajustamos para o horizonte de tempo desejado usando a regra da raiz quadrada do tempo. Essa regra nos permite projetar o risco de 1 dia para múltiplos dias (assumindo que os retornos são independentes).
O Método Histórico: Aprendendo com o Passado
Diferente do método paramétrico, a abordagem histórica não faz nenhuma suposição sobre a distribuição dos retornos. Ela simplesmente olha para o passado e assume que o futuro se comportará de forma semelhante. É um método mais direto e robusto a distribuições não-normais.
# ==============================================================================
# 4. FUNÇÃO: CÁLCULO DO VaR E CVaR HISTÓRICO
# ==============================================================================
def calcular_var_cvar_historico(retornos_portfolio, confianca, horizonte_dias):
"""Calcula o VaR e CVaR Histórico para o horizonte de dias."""
# VaR Histórico: O percentil dos retornos
var_hist = retornos_portfolio
var_hist_perda = -var_hist * np.sqrt(horizonte_dias)
return var_hist_perda
O cálculo é muito intuitivo:
1.VaR Histórico: Usamos a função quantile(1 – confianca) para encontrar o retorno que corresponde ao nosso percentil de perda. Por exemplo, para 95% de confiança, procuramos o quantil 0.05, que representa os 5% piores retornos históricos.
2.CVaR Histórico: Esta é a parte mais interessante. Primeiro, filtramos todos os retornos que foram piores que o nosso VaR Histórico (retornos_portfolio < var_hist). Em seguida, simplesmente calculamos a média (mean()) desses retornos. O resultado é a perda média nos piores 5% dos casos.
Com essas três métricas (VaR Paramétrico, VaR Histórico e CVaR Histórico) calculadas, temos uma visão multifacetada do risco da nossa carteira. Mas números por si só não contam a história completa. Precisamos visualizá-los.
Se você quer levar sua análise de investimentos para o próximo nível? Uma corretora com plataformas avançadas pode oferecer algumas ferramentas que você precisa para aplicar esses conceitos.
Parte 4: Visualizando o Risco: O Dashboard Completo
Uma análise de risco, por mais precisa que seja, perde muito do seu valor se não for comunicada de forma clara e eficaz. É por isso que a visualização de dados é uma etapa indispensável. Nosso código não apenas calcula o VaR e o CVaR, mas também gera um dashboard completo para que possamos interpretar os resultados de maneira intuitiva.
Este código é extremamente grande, sendo assim estarei inserindo a penas um trecho, entre em contato para obter.
# ==============================================================================
# 5. FUNÇÃO: VISUALIZAÇÕES COMPLETAS
# ==============================================================================
def criar_visualizacoes_completas(retornos_portfolio, pesos, var_param, var_hist, cvar_hist, confianca, horizonte_dias, ativos):
""" Cria visualizações completas para análise de risco do portfólio """
# Configuração do estilo
plt.style.use('seaborn-v0_8')
fig = plt.figure(figsize=(20, 16))
# 6.1. Distribuição de Retornos e VaR
ax1 = plt.subplot2grid((3, 3), (0, 0), colspan=2)
plotar_distribuicao_var(retornos_portfolio, var_param, var_hist, cvar_hist, confianca, ax1)
# 6.2. Composição do Portfólio
ax2 = plt.subplot2grid((3, 3), (0, 2))
plotar_composicao_portfolio(pesos, ativos, ax2)
# 6.3. Série Temporal dos Retornos
ax3 = plt.subplot2grid((3, 3), (1, 0), colspan=3)
plotar_serie_temporal(retornos_portfolio, ax3)
# 6.4. Comparação de Métodos VaR
ax4 = plt.subplot2grid((3, 3), (2, 0))
plotar_comparacao_var(var_param, var_hist, cvar_hist, horizonte_dias, ax4)
# 6.5. Histograma Detalhado
ax5 = plt.subplot2grid((3, 3), (2, 1), colspan=2)
plotar_histograma_detalhado(retornos_portfolio, var_param, var_hist, cvar_hist, confianca, ax5)
# ... (código das 5 subtramas/plots) ...
plt.tight_layout()
plt.show()
A função criar_visualizacoes_completas orquestra a criação de seis gráficos diferentes, cada um oferecendo uma peça do quebra-cabeça da análise de risco. Vamos analisar o que cada um deles nos mostra.
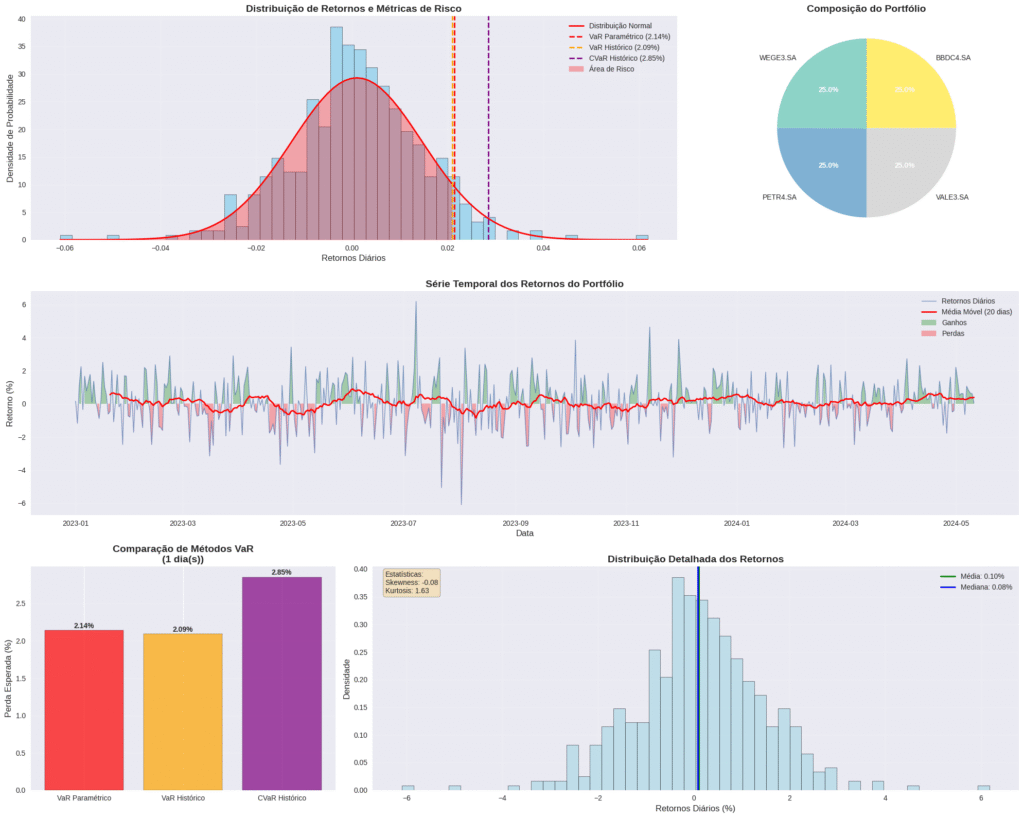
Dashboard de análise e risco VaR e CVaR com 6 gráficos mostrando distribuição de retornos, composição de portfólio, série temporal, comparação de métodos e estatística minuciosa.
Sistema de análise de risco com VaR Paramétrico, VaR Histórico e CVaR Histórico aplicado a um portfólio de ações brasileiras.
1. Distribuição de Retornos e Métricas de Risco
Este é o gráfico principal do nosso dashboard. Ele nos mostra a distribuição histórica dos retornos diários da nossa carteira (o histograma em azul) e a compara com uma distribuição normal teórica (a linha vermelha). As linhas verticais pontilhadas marcam os valores calculados para o VaR Paramétrico, VaR Histórico e CVaR Histórico. A área sombreada em vermelho representa a “Área de Risco”, destacando visualmente a cauda esquerda da distribuição, onde ocorrem as perdas.
Este gráfico é poderoso porque nos permite ver de relance se os retornos da nossa carteira se comportam como o esperado pelo modelo paramétrico e quão distantes estão as métricas de risco umas das outras.
2. Composição do Portfólio
Um simples, mas essencial, gráfico de pizza. Ele mostra a alocação de capital entre os diferentes ativos da carteira. Em nosso caso, com pesos iguais, vemos uma divisão perfeita de 25% para cada ativo. Este gráfico é fundamental para entendermos de onde vêm os riscos e retornos.
3. Série Temporal dos Retornos do Portfólio
Este gráfico plota os retornos diários da carteira ao longo do tempo. As áreas verdes representam os dias de ganho, e as vermelhas, os dias de perda. A linha vermelha mais grossa é uma média móvel de 20 dias, que ajuda a suavizar a volatilidade e a identificar tendências de curto prazo no desempenho do portfólio. Ele nos dá uma noção da volatilidade e do comportamento da carteira em diferentes períodos.
4. Comparação de Métodos VaR
Este gráfico de barras coloca lado a lado os valores de VaR Paramétrico, VaR Histórico e CVaR Histórico. É uma das visualizações mais importantes para a tomada de decisão. Aqui podemos comparar diretamente a perda esperada segundo os diferentes modelos. Note como o CVaR Histórico é sempre maior que os VaRs, pois ele representa a média das perdas além do VaR, capturando o risco de eventos mais extremos.
5. Distribuição Detalhada dos Retornos
Este histograma foca em estatísticas descritivas mais detalhadas. Além de mostrar a distribuição dos retornos, ele marca a média e a mediana e exibe em uma caixa de texto duas métricas cruciais:
• Skewness (Assimetria): Mede a assimetria da distribuição. Um valor negativo, como no nosso caso (-0.08), indica uma leve “cauda” para a esquerda, sugerindo que grandes perdas são um pouco mais prováveis que grandes ganhos.
• Kurtosis (Curtose): Mede o quão “pesadas” são as caudas da distribuição. Uma curtose maior que a da distribuição normal (que é 0 para a curtose em excesso) indica que eventos extremos (grandes ganhos ou perdas) são mais prováveis do que o modelo normal sugere. No nosso caso, o valor de 1.63 indica caudas mais pesadas.
Essas estatísticas nos ajudam a entender por que o VaR Paramétrico, que assume uma distribuição normal, pode subestimar o risco real.
6. Resumo da Análise de Risco (Saída de Texto)
Por fim, o código gera uma tabela de resumo com as principais métricas do portfólio, como retorno médio, volatilidade (desvio padrão), Sharpe Ratio e os valores percentuais exatos para VaR e CVaR. É o complemento quantitativo perfeito para a análise visual.
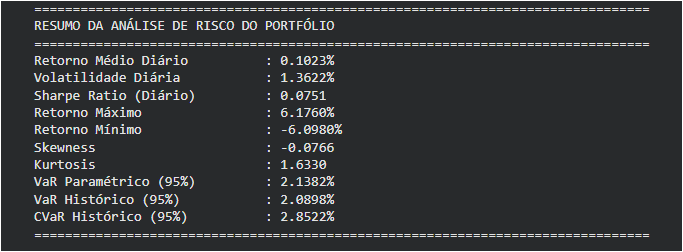
Este resumo nos diz, por exemplo, que com 95% de confiança, não deveríamos esperar perder mais de 2.09% (VaR Histórico) em um único dia. No entanto, nos 5% piores dias, a perda média esperada é de 2.85% (CVaR Histórico).
Sua carteira está preparada para os piores cenários? Um consultor financeiro pode ajudá-lo a construir um portfólio resiliente e alinhado aos seus objetivos. Agende uma conversa sem compromisso com seu consultor financeiro e proteja seu patrimônio!
De Dados a Decisões, o Poder do VaR e CVaR
Ao longo deste artigo, transformamos conceitos complexos de gestão de risco em um sistema prático e funcional utilizando Python. Partimos da teoria, entendendo a diferença fundamental entre Value at Risk (VaR) e Conditional Value at Risk (CVaR), e chegamos a um dashboard completo que não apenas calcula, mas também ilustra o risco de um portfólio de investimentos de maneira clara e acionável.
Demonstramos que, enquanto o VaR estabelece um limite para perdas em cenários normais, o CVaR nos prepara para o inesperado, quantificando a magnitude das perdas em eventos extremos. A combinação dessas duas métricas, calculadas tanto pelo método paramétrico quanto pelo histórico, oferece uma visão de risco muito mais robusta do que qualquer uma delas isoladamente.
O código que desenvolvemos é um ponto de partida poderoso. Ele pode ser expandido para incluir diferentes ponderações de ativos (em vez de pesos iguais), incorporar outras classes de ativos, testar diferentes níveis de confiança e até mesmo implementar o método de Simulação de Monte Carlo para o cálculo do VaR, uma abordagem ainda mais flexível.
A verdadeira maestria em investimentos não está em evitar o risco, mas em compreendê-lo, medi-lo e gerenciá-lo de forma proativa. Ferramentas como o sistema de análise de VaR e CVaR que construímos são essenciais nesse processo, permitindo que investidores e gestores tomem decisões mais informadas, protejam seu capital e naveguem pelos mercados com mais confiança e estratégia.
Pronto para aplicar uma gestão de risco profissional em seus investimentos? Explore plataformas de negociação que oferecem ferramentas analíticas avançadas e comece a tomar decisões baseadas em dados. Descubra as melhores plataformas para traders e investidores!
FAQs
Por que o VaR Paramétrico (Gaussiano) frequentemente subestima o risco real do meu portfólio?
O VaR Paramétrico assume que os retornos do seu portfólio seguem a distribuição normal (Curva de Sino). No entanto, o mercado financeiro é caracterizado por curtose elevada (“caudas pesadas”), o que significa que eventos extremos (grandes perdas) ocorrem com mais frequência do que o modelo normal prevê. Se o seu portfólio tiver curtose positiva, o VaR Paramétrico dará uma falsa sensação de segurança.
O que as métricas Skewness (Assimetria) e Kurtosis (Curtose) do meu portfólio me dizem sobre o risco de cauda?
Skewness (Assimetria): Um valor negativo, como no seu artigo, indica que a distribuição de retornos tem uma cauda mais longa para o lado esquerdo (perdas). Isso sugere que grandes perdas são mais prováveis do que grandes ganhos, confirmando a necessidade de usar o CVaR.
Kurtosis (Curtose): Um valor positivo acima de 0 (em excesso), como o 1.63 do seu exemplo, confirma que a distribuição tem caudas mais pesadas do que a distribuição normal. Isso significa que há uma maior probabilidade de eventos extremos (outliers), tornando o VaR Histórico/CVaR mais confiáveis que o VaR Paramétrico.
Por que o CVaR é considerado uma métrica de risco “coerente” e mais utilizada na otimização de portfólios que o VaR?
O CVaR possui a propriedade de subaditividade, uma característica de medidas de risco “coerentes”. Na prática, isso significa que o risco de uma carteira combinada é sempre menor ou igual à soma dos riscos de seus ativos individuais. O VaR falha neste ponto (não é subaditivo), o que pode levar a decisões que, ironicamente, aumentam o risco total ao invés de gerenciá-lo. Além disso, o CVaR é mais fácil de otimizar matematicamente.
O que é Backtesting e como posso usá-lo para saber se o meu modelo de VaR em Python está funcionando corretamente?
Backtesting é o processo de comparar as perdas reais do portfólio no passado com as perdas projetadas pelo modelo VaR. Se você usa um VaR de 95%, você espera que a perda real exceda o VaR em aproximadamente 5% dos dias (ou seja, 5 “violações” em 100 dias). Se o número de violações for muito maior que 5%, seu modelo está subestimando o risco e precisa ser ajustado.
O CVaR sempre será maior que o VaR? Por quê?
Sim, o CVaR será sempre maior ou igual ao VaR. Isso acontece porque o VaR marca o ponto de corte, enquanto o CVaR é a média de todas as perdas que estão além desse ponto de corte. Como o CVaR inclui as perdas mais extremas (o “pior do pior”), sua magnitude será necessariamente maior, oferecendo uma estimativa de risco mais conservadora.
O que significa um VaR de 95% de 2% para um portfólio de R$ 100.000?
Significa que há apenas 5% de chance (o inverso do nível de confiança de 95%) de você perder mais de R$ 2.000,00 (2% de R$ 100.000) no período analisado (geralmente 1 dia, como no artigo). Em outras palavras, você espera que, em 95 dias de 100, sua perda não ultrapasse R$ 2.000,00.
Qual a principal diferença prática entre VaR e CVaR (Expected Shortfall)?
O VaR informa a perda máxima que você não deve esperar ultrapassar em um determinado percentual do tempo (ex: 95% dos dias). O CVaR (Perda Esperada) vai além: ele calcula a perda média esperada nos piores cenários, ou seja, quando a perda já excedeu o limite do VaR (os 5% piores dias, por exemplo). O CVaR é uma métrica mais cautelosa para o risco de cauda (eventos extremos).