Aprofundando a Análise
No artigo anterior, exploramos os fundamentos das Distribuições Normal e Lognormal, bem como a importância dos Retornos Empíricos para o investidor leigo. Agora, vamos aprofundar esses conceitos, desvendando as nuances e as aplicações mais sofisticadas que são cruciais para quem busca uma compreensão mais robusta do mercado financeiro. Para o investidor intermediário, ir além do básico significa entender as limitações dos modelos e como a realidade do mercado se desvia das premissas teóricas, permitindo uma análise de risco e otimização de portfólio mais eficaz.
O mercado financeiro é um ambiente complexo, onde a aleatoriedade e a racionalidade se entrelaçam. As distribuições estatísticas servem como lentes através das quais podemos tentar decifrar essa complexidade. Contudo, é vital reconhecer que nenhum modelo é perfeito, e a verdadeira maestria reside em compreender as deficiências de cada ferramenta e como compensá-las. Este artigo visa equipá-lo com um conhecimento mais aprofundado sobre como as distribuições se comportam na prática e como os retornos empíricos revelam a verdadeira face da volatilidade e do risco.
A Distribuição Normal: Limitações e o Fenômeno das Caudas Pesadas
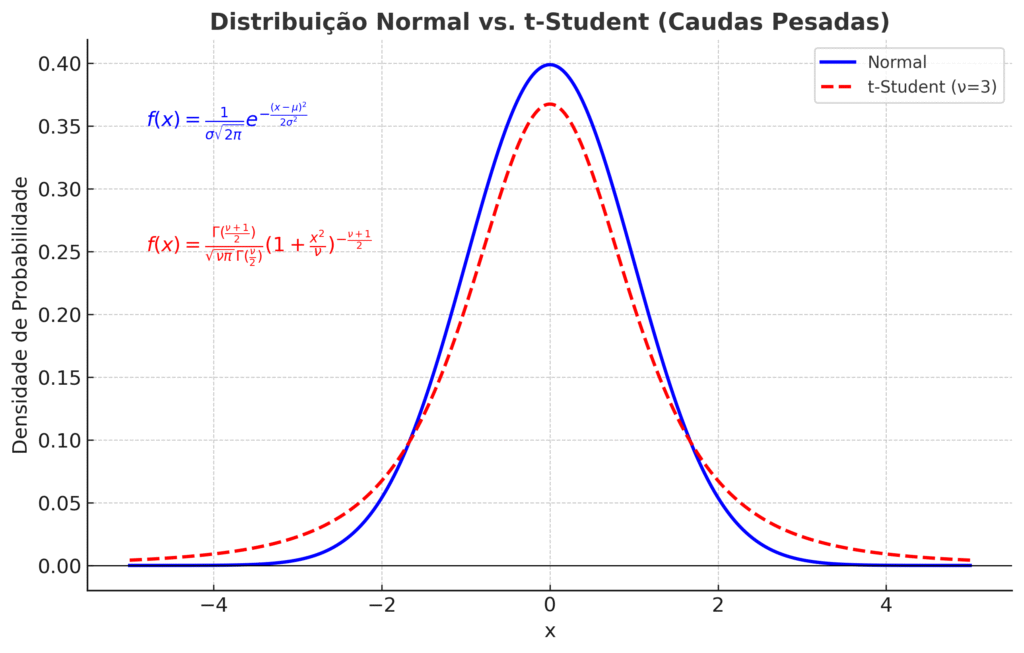
No artigo para leigos, apresentamos a Distribuição Normal como um modelo fundamental para os retornos de ativos. No entanto, para o investidor intermediário, é crucial entender suas limitações, especialmente no contexto do mercado financeiro. A premissa de que os retornos seguem uma distribuição normal implica que eventos extremos (grandes quedas ou altas) são raros e previsíveis. Contudo, a realidade empírica do mercado financeiro frequentemente contradiz essa premissa.
O fenômeno das “caudas pesadas” (fat tails), ou leptocurtose, é uma das principais falhas da Distribuição Normal na modelagem de retornos financeiros. Isso significa que eventos de grande magnitude (tanto positivos quanto negativos) ocorrem com uma frequência muito maior do que o previsto pela curva normal. Em outras palavras, o mercado financeiro é propenso a “cisnes negros” – eventos raros e de alto impacto que não são bem capturados por uma distribuição gaussiana. Essa característica é visível na curtose dos retornos, que é significativamente maior do que o valor 3 esperado para uma distribuição normal.
Além das caudas pesadas, os retornos financeiros também exibem assimetria (skewness), ou seja, a distribuição não é perfeitamente simétrica em torno da média. Frequentemente, observa-se uma assimetria negativa (cauda esquerda mais longa), indicando que grandes perdas são mais prováveis do que grandes ganhos de mesma magnitude. Essa assimetria e as caudas pesadas são “fatos estilizados” dos retornos financeiros, que exigem a consideração de modelos estatísticos mais robustos para uma gestão de risco eficaz.
A Distribuição Lognormal e o Modelo de Black-Scholes
A Distribuição Lognormal, como vimos, é mais adequada para modelar os preços dos ativos, pois garante que os preços permaneçam não negativos e reflete a natureza multiplicativa dos retornos. Sua importância se eleva exponencialmente quando consideramos a precificação de opções e outros derivativos. O famoso Modelo de Black-Scholes, um pilar da precificação de opções, assume que os preços dos ativos subjacentes seguem um processo estocástico com retornos lognormalmente distribuídos.
Este modelo, embora revolucionário, também possui suas limitações, muitas delas decorrentes da própria premissa da lognormalidade e da normalidade dos retornos contínuos. Por exemplo, o modelo de Black-Scholes tende a subestimar os preços de opções fora do dinheiro (out-of-the-money) e superestimar os preços de opções dentro do dinheiro (in-the-money), um fenômeno conhecido como “sorriso de volatilidade” (volatility smile). Isso ocorre porque o modelo não captura adequadamente as caudas pesadas e a assimetria observadas nos retornos empíricos.
Para o investidor intermediário, entender a relação entre a Distribuição Lognormal e o modelo de Black-Scholes é crucial para compreender os fundamentos da precificação de derivativos e as razões pelas quais as volatilidades implícitas no mercado se desviam da volatilidade histórica, refletindo as expectativas dos participantes do mercado sobre eventos extremos.
Retornos Empíricos: Fatos Estilizados e Implicações Práticas
Os retornos empíricos são a fonte primária de dados para a análise financeira e, ao contrário dos modelos teóricos, refletem a realidade do mercado. A análise aprofundada dos retornos empíricos revela uma série de “fatos estilizados” que são consistentes em diferentes mercados e períodos de tempo. Além das já mencionadas caudas pesadas e assimetria, outros fatos estilizados incluem:
• Agrupamento de Volatilidade (Volatility Clustering): Períodos de alta volatilidade tendem a ser seguidos por períodos de alta volatilidade, e períodos de baixa volatilidade por períodos de baixa volatilidade. Isso sugere que a volatilidade não é constante ao longo do tempo, o que contraria uma das premissas de modelos como o Black-Scholes.
• Ausência de Correlação Serial nos Retornos (Exceto em Altas Frequências): Em horizontes de tempo mais longos (dias, semanas), os retornos de ativos financeiros são aproximadamente não correlacionados, o que apoia a Hipótese do Mercado Eficiente em sua forma fraca. No entanto, em frequências muito altas (milissegundos, segundos), pequenas correlações podem ser observadas.
• Efeito Alavancagem (Leverage Effect): Quedas nos preços dos ativos tendem a ser acompanhadas por um aumento na volatilidade futura, enquanto aumentos nos preços são acompanhados por uma diminuição na volatilidade. Isso pode ser explicado pelo aumento do endividamento relativo das empresas após uma queda no preço das ações, o que aumenta o risco percebido.
Implicações Práticas:
Para o investidor intermediário, a compreensão desses fatos estilizados é crucial para:
1.Gestão de Risco: Modelos de risco que assumem normalidade podem subestimar o risco de eventos extremos. A incorporação de distribuições com caudas mais pesadas (como a t-Student ou distribuições estáveis) ou o uso de modelos GARCH (Generalized Autoregressive Conditional Heteroskedasticity) para capturar o agrupamento de volatilidade são abordagens mais realistas.
2.Otimização de Portfólio: A otimização de portfólio baseada apenas na média e variância (como no modelo de Markowitz) pode ser inadequada se os retornos não forem normais. Considerar a assimetria e a curtose na otimização pode levar a portfólios mais robustos e eficientes.
3.Precificação de Derivativos: A não normalidade dos retornos empíricos explica as deficiências de modelos como o Black-Scholes e impulsiona o desenvolvimento de modelos mais avançados que incorporam saltos (jumps) ou volatilidade estocástica.
Em suma, os retornos empíricos nos fornecem a “verdade” do mercado, e é a partir de sua análise que os modelos teóricos são desafiados, aprimorados e adaptados para refletir a complexidade do mundo financeiro real.
Conclusão
Para o investidor intermediário, a jornada de compreensão das distribuições estatísticas no mercado financeiro vai além da simples definição. É fundamental reconhecer as limitações da Distribuição Normal e da Lognormal diante dos fatos estilizados dos retornos empíricos, como as caudas pesadas, a assimetria e o agrupamento de volatilidade. Essa compreensão aprofundada permite uma análise de risco mais precisa, a construção de portfólios mais resilientes e uma avaliação mais crítica dos modelos de precificação de ativos e derivativos.
O mercado financeiro é dinâmico e complexo, e a aplicação de modelos estatísticos deve ser feita com discernimento, sempre confrontando a teoria com a realidade empírica. Ao dominar esses conceitos e suas implicações práticas, você estará mais apto a navegar pelas incertezas do mercado, otimizar suas estratégias de investimento e tomar decisões mais informadas e sofisticadas.
Referências
Maxwell, PUC-Rio. 2 Distribuições de Probabilidade.
Leia também:
Distribuições Estatísticas no Mercado Financeiro para Leigos: Entenda o Básico
Episodio 5 – Os Maiores Erros de Warren Buffett e as Lições Inestimáveis para Investidores